Es posible factorizar expresiones que involucran funciones trigonométricas mediante los mismos métodos que se utilizan en la factorización de polinomios.
Factor común
En este caso es necesario identificar un factor común que aparezca en todos los términos y aplicar la propiedad distributiva.
Factor común por agrupación
En este se separa la expresión en dos o más partes iguales (igual cantidad de terminos). En cada una de ellas, se identifica el factor común y se aplica la propiedad distrivutiva.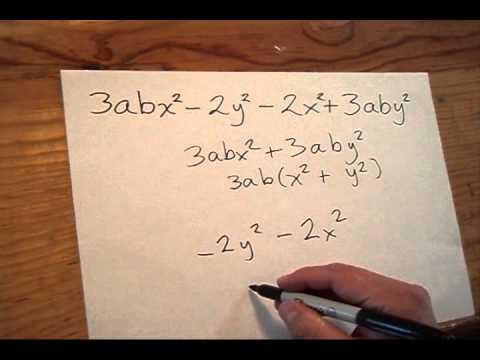
Diferencia de cuadrados
La diferencia de cuadrado de 2 expresiones que involucran funciones trigonométricas es igual al producto de la suma por la diferencia de las 2 expresiones, cómo se muestra en el siguiente ejemplo:
Trinomio cuadrado perfecto
En este cualquier suma de binomios al cuadrado es igual al cuadrado del primer término, más el doble del primer por el segundo término, más el cuadrado del segundo término.
Trinomio de la form X2 +bx+ c
Para factorizar un trinomio de esta forma, se buscan 2 números r y s cuyo producto sea igual a C y su suma igual a b.
Simplificación
Para simplificar una fracción en la que el numerador y denominador son productos de funciones trigonométricas se aplica la propiedad de potencia de igual base.
un concepto de todo esto por favor
ResponderEliminar