Ir al contenido principal

DEFINICION DE LAS FUNCIONES TRIGONOMETRICAS DE UN ANGULO EN POSICION NORMAL

Si teta es un ángulo en posición normal y p(x,y) es cualquier punto contenido en el lado final diferente de 0(0,0)cumple que px op=r = raiz de x a la dos + y a la dos. 
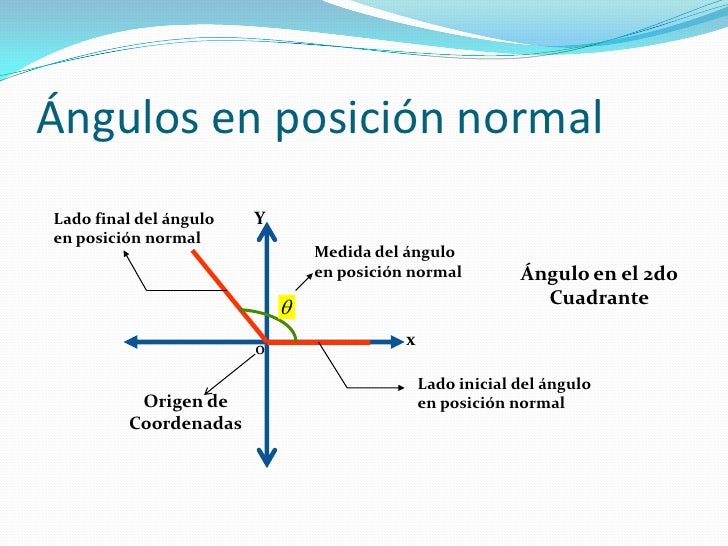
 Se define las funciones trigonométricas para el ángulo teta de la siguiente manera:


Resultado de imagen para DEFINICION DE LAS FUNCIONES TRIGONOMETRICAS DE UN ANGULO EN POSICION NORMAL

El  valor de las funciones trigonométricas de un ángulo teta es independiente del punto que se ubique sobre su lado final en la siguiente una sé inicia gráfica que demuestra esta afirmación los 2triángulos O, R, Q y O, S, P son semejantes los rectángulos
.
Cabe notar que las funciones tangente y secantes de teta no están definidas para los ángulos + π/2 O + 3π/2 De la misma manera las funciones cotangente y cosecante no están definidas para los ángulos 0, ,π, + 2π

Comentarios

Publicar un comentario

Entradas populares de este blog

ANGULOS SOBRE EL PLANO CARTESIANO

Un ángulo se considera en posición canónica  o normal si su lado inicial es el semi eje positivo de las X y su vértice es el origen. Cuando un ángulo se encuentra en posición normal, la ubicación del lado final indica a qué cuadrante pertenece el ángulo. . . Dos ángulos en posición normal pueden tener el mismo lado final, en este caso se dicen que los ángulos son coterminales .
2 comentarios
Leer más

FACTORIZACION DE EXPRESIONES TRIGONOMETRICAS

Es posible factorizar expresiones que involucran funciones trigonométricas mediante los mismos métodos que se utilizan en la factorización de polinomios. Factor común En este caso es necesario identificar un factor común que aparezca en todos los términos y aplicar la propiedad distributiva. Factor común por agrupación En este se separa la expresión en dos o más partes iguales (igual cantidad de terminos). En cada una de ellas, se identifica el factor común y se aplica la propiedad distrivutiva. Diferencia de cuadrados La diferencia de cuadrado de 2 expresiones que involucran funciones trigonométricas es igual al producto de la suma por la diferencia de las 2 expresiones, cómo se muestra en el siguiente ejemplo: Trinomio cuadrado perfecto En este cualquier suma de binomios al cuadrado es igual al cuadrado del primer término, más el doble del primer por el segundo término, más el cuadrado del segundo término. Trinomio de la form X 2  +bx+ c Para
1 comentario
Leer más